---
title: "Your turn - Lesson 8"
author: "Analyzing Categorical Data"
output:
html_document:
css: http://www.bradthiessen.com/batlab2.css
highlight: pygments
theme: spacelab
fig_width: 5.6
fig_height: 4
---
*****
**Author(s):** [Enter names of people working on these solutions]
*****
```{r message=FALSE, echo=FALSE}
# Above, type your name in the "Author(s)" section
# Load the mosaic package
library(mosaic)
require(ggplot2)
```
# Your turn
19. Criminologists have long debated whether there is a relationship between weather conditions and the incidence of violent crime. The article *Is There a Season for Homocide?* (Criminology, 1988: 287-296) classified 1361 homicides according to season, resulting in table displayed below. Conduct a chi-square goodness-of-fit test (and the randomization-based chi-square test) to determine if seasons are associated with different numbers of violent crimes.

```{r}
# Input frequencies
crimes <- c(328, 334, 372, 327)
# Input the expected probabilities for each season
# Replace the XXXXX values with your expected probabilities
probs <- c(XXXXX, XXXXX, XXXXX, XXXXX)
# Run the chi-square test using chisq.test
# Replace the XXXXX with the name of your frequencies data
# Replace the YYYYY with the name of your probabilities
chisq.test(XXXXX, p = YYYYY, rescale.p = TRUE)
# Randomization-based chi-square test
chisq.test(XXXXX, p = YYYYY, rescale.p = TRUE, simulate.p.value = TRUE, B=5000)
```
**Write conclusion here**
20. You may remember the dataset we analyzed in [lesson #3](http://bradthiessen.com/html5/stats/m301/lab3.html) regarding the amount of weight lost by subjects on various diets (e.g., Atkins, WeightWatchers). Prior to analyzing that data, we tested the homogeneity of variance assumption with Levene's test. Let's test for normality using a chi-square goodness-of-fit test.
```{r}
# Input data
diet <- read.csv("http://www.bradthiessen.com/html5/data/diet.csv")
# Store data as "weight"
weight <- diet$WeightLoss
# Create histogram
histogram(~weight, col="lightblue", border="white")
# This will cut the data into 6 bins
# The bins are:
# 4+ lbs gained, 0-4 lbs gained, 0-4 lbs lost,
# 4-8 lbs lost, 8-12 lbs lost, 12+ lbs lost
cuts <- cut(weight, breaks = c(-Inf, -4, 0, 4, 8, 12, Inf), labels=c("gained 4+ lbs", "gained 0-4 lbs", "lost 0-4 lbs", "lost 4-8 lbs", "lost 8-12 lbs", "lost 12+ lbs"))
# This will show the table of frequencies
tally(~cuts, margins=TRUE)
# This will store the frequencies within each bin as "weightbins"
weightbins <- c(length(cuts[cuts=="gained 4+ lbs"]),
length(cuts[cuts=="gained 0-4 lbs"]),
length(cuts[cuts=="lost 0-4 lbs"]),
length(cuts[cuts=="lost 4-8 lbs"]),
length(cuts[cuts=="lost 8-12 lbs"]),
length(cuts[cuts=="lost 12+ lbs"]))
# Look at those frequencies to match the table we displayed above
weightbins
# Calculate normal probabilities for each bin
# Weights ~ normal(mean, sd)
p1 <- pnorm(-4, mean=mean(weight), sd=sd(weight), lower.tail = TRUE) #P(x < -4)
p2 <- pnorm(0, mean=mean(weight), sd=sd(weight))-pnorm(-4, mean=mean(weight), sd=sd(weight))
p3 <- pnorm(4, mean=mean(weight), sd=sd(weight))-pnorm(0, mean=mean(weight), sd=sd(weight))
p4 <- pnorm(8, mean=mean(weight), sd=sd(weight))-pnorm(4, mean=mean(weight), sd=sd(weight))
p5 <- pnorm(12, mean=mean(weight), sd=sd(weight))-pnorm(8, mean=mean(weight), sd=sd(weight))
p6 <- pnorm(12, mean=mean(weight), sd=sd(weight), lower.tail = FALSE) #P(X > 12)
p1+p2+p3+p4+p5+p6
# Store all the probabilities as "probs"
probs <- c(p1, p2, p3, p4, p5, p6)
# Now run the chi-squared test
chisq.test(weightbins, p = probs)
# Next with randomization-based methods
chisq.test(weightbins, p = probs, simulate.p.value = TRUE, B=5000)
```
**WRITE YOUR CONCLUSIONS HERE**
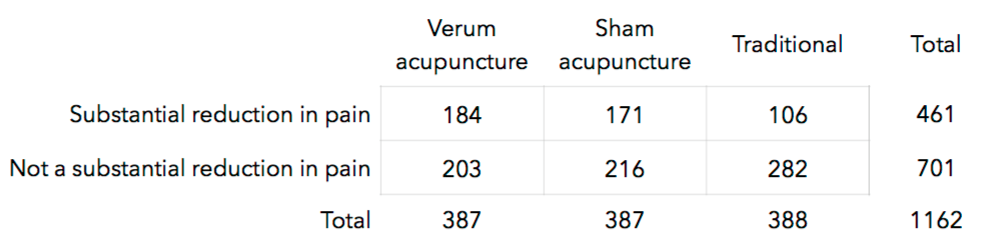
21. Is acupuncture effective in reducing pain? A [2007 study](http://www.ncbi.nlm.nih.gov/pubmed/17893311) looked at 1,162 patients with chronic lower back pain. The subjects were randomly assigned to one of 3 groups:
• **Verum acupuncture** practiced according to traditional Chinese principles,
• **Sham acupuncture** where needles were inserted into the skin but not at acupuncture points,
• **Traditional** (non-acupuncture) therapy consisting of drugs, physical therapy, and exercise.
Results are displayed in the table below.
**(a)** Calculate the probability that an individual undergoing verum acupuncture experienced a substantial reduction in pain.
**(b)** Calculate this same probability for the subjects in the traditional group.
**(c)** Calculate and interpret the ratio of the two probabilities you just calculated.
**(d)** Run a chi-square test for independence and interpret the result.
 ```{r}
# Input data and store in data.frame called "acupuncture"
pain <- c(rep("reduced", 184), rep("not", 203), rep("reduced", 171), rep("not", 216), rep("reduced", 106), rep("not", 282))
treatment <- c(rep("verum", 387), rep("sham", 387), rep("traditional", 388))
acupuncture <- data.frame(treatment, pain)
# Show a table of the frequencies
tally(pain ~ treatment, data=acupuncture, margins=TRUE)
# Run the chi-square test
chisq.test(acupuncture$treatment, acupuncture$pain, correct=FALSE)
```
```{r}
# Input data and store in data.frame called "acupuncture"
pain <- c(rep("reduced", 184), rep("not", 203), rep("reduced", 171), rep("not", 216), rep("reduced", 106), rep("not", 282))
treatment <- c(rep("verum", 387), rep("sham", 387), rep("traditional", 388))
acupuncture <- data.frame(treatment, pain)
# Show a table of the frequencies
tally(pain ~ treatment, data=acupuncture, margins=TRUE)
# Run the chi-square test
chisq.test(acupuncture$treatment, acupuncture$pain, correct=FALSE)
```
**WRITE YOUR CONCLUSIONS HERE**
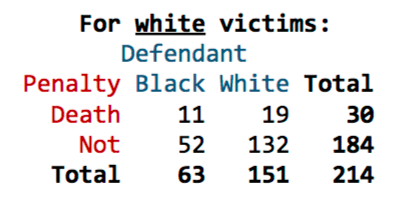
22. The table displayed below shows the number of black and white defendants sentenced to death in the 1960s-70s for murdering a white victim. As you can see, a higher proportion of black defendants were sentenced to death.
**(a)** Run Fisher's Exact Test to calculate the likelihood of observing results as or more extreme than these results if, in fact, race and the death penalty were independent.
**(b)** Run a chi-square test for independence.
 ```{r}
# Input data
race <- c(rep("white", 151), rep("black", 63))
death <- c(rep("yes", 19), rep("no", 132), rep("yes", 11), rep("no", 52))
deathpenalty <- data.frame(race, death)
# Show table of frequencies
tally(death ~ race, data=deathpenalty, margins=TRUE)
# Run a Fisher's exact test (follow the syntax in the lesson)
fisher.test()
# Run a chi-square test (follow the syntax in the lesson)
chisq.test()
```
```{r}
# Input data
race <- c(rep("white", 151), rep("black", 63))
death <- c(rep("yes", 19), rep("no", 132), rep("yes", 11), rep("no", 52))
deathpenalty <- data.frame(race, death)
# Show table of frequencies
tally(death ~ race, data=deathpenalty, margins=TRUE)
# Run a Fisher's exact test (follow the syntax in the lesson)
fisher.test()
# Run a chi-square test (follow the syntax in the lesson)
chisq.test()
```

 ```{r}
# Input data and store in data.frame called "acupuncture"
pain <- c(rep("reduced", 184), rep("not", 203), rep("reduced", 171), rep("not", 216), rep("reduced", 106), rep("not", 282))
treatment <- c(rep("verum", 387), rep("sham", 387), rep("traditional", 388))
acupuncture <- data.frame(treatment, pain)
# Show a table of the frequencies
tally(pain ~ treatment, data=acupuncture, margins=TRUE)
# Run the chi-square test
chisq.test(acupuncture$treatment, acupuncture$pain, correct=FALSE)
```
```{r}
# Input data and store in data.frame called "acupuncture"
pain <- c(rep("reduced", 184), rep("not", 203), rep("reduced", 171), rep("not", 216), rep("reduced", 106), rep("not", 282))
treatment <- c(rep("verum", 387), rep("sham", 387), rep("traditional", 388))
acupuncture <- data.frame(treatment, pain)
# Show a table of the frequencies
tally(pain ~ treatment, data=acupuncture, margins=TRUE)
# Run the chi-square test
chisq.test(acupuncture$treatment, acupuncture$pain, correct=FALSE)
```
 ```{r}
# Input data
race <- c(rep("white", 151), rep("black", 63))
death <- c(rep("yes", 19), rep("no", 132), rep("yes", 11), rep("no", 52))
deathpenalty <- data.frame(race, death)
# Show table of frequencies
tally(death ~ race, data=deathpenalty, margins=TRUE)
# Run a Fisher's exact test (follow the syntax in the lesson)
fisher.test()
# Run a chi-square test (follow the syntax in the lesson)
chisq.test()
```
```{r}
# Input data
race <- c(rep("white", 151), rep("black", 63))
death <- c(rep("yes", 19), rep("no", 132), rep("yes", 11), rep("no", 52))
deathpenalty <- data.frame(race, death)
# Show table of frequencies
tally(death ~ race, data=deathpenalty, margins=TRUE)
# Run a Fisher's exact test (follow the syntax in the lesson)
fisher.test()
# Run a chi-square test (follow the syntax in the lesson)
chisq.test()
```